開篇宣告:1:以下內容轉自以下內容轉自微信公眾號大家的風研信:
【人間的統計學】聊聊各種分佈1:讓你不白努力的白努力分佈及其變身後的二項分佈,如有侵權,可聯絡刪除
2. 以下觀點,僅代表作者個人觀點,請帶著質疑的態度去閱讀。如有問題,歡迎評論區留言或直接聯絡作者
【人間的統計學】聊聊各種分佈1:讓你不白努力的白努力分佈及其變身後的二項分佈
第一次看到“白努力”這個名字的時候,突然感覺打通了東西方文化的壁壘。我們老家就流傳著“起賤名,好養活”的說法。所以,周圍有好多“鐵蛋”,“狗剩”,“二丫”之類的小名。以至於我總尋思,如果我爸媽給我起個小名叫“瞎忙活”,會不會就能有更多的學術成就了。唉。儘管如此,我還是淺薄了。後來知道人家“白努力"是姓,而不是名。咱的文化裡,就算是改名,也改不了姓啊。或許,等某一天,我人生蓋棺定論時,可以在墓碑上寫上“蔣·瞎忙活·新宇”。在形式上,與偉大的人物對齊。哈哈哈哈。(Bernoulli distribution,官方翻譯應該是伯努利分佈。但你可以想象東北口音把“伯”重讀成“白”的感覺,直到走出東北之前,我都一直白努力白努力的......)
拉回來,說正經的。我們到處都見到的“白努力”,可能不是一個人。白努力是瑞士的一個商人和學者家族。這個家族經常出現在書本上的有三個人,哥哥雅各布白努力,對,這個是我們機率統計裡面正牌的白努力,以白努力分佈而聞名。弟弟約翰白努力,大數學家,以最速降線聞名。他應該沒有他哥哥那麼有名。但他有個很厲害的學生,就是大神尤拉(哇,大神尤拉的老師啊)。他還有一個很優秀的兒子,丹尼爾白努力,嗯,就是流體力學的白努力定理的那個白努力。這種“一門三學士,師徒皆大家”的感覺,跟我偶像蘇東坡他家一模一樣。
好了,我們回到雅各布的白努力分佈(Bernoulli distribution)吧。白努力分佈是一個離散型機率分佈,又叫兩點分佈或者0-1分佈。定義如下:
如果一個隨機變數 只能取值0和1,並且機率為 和 , ,則隨機變數 具有引數為 的白努力分佈。我們還可以用一種更帥氣的方式表達:
這是數學的表達的魅力,一個公式把兩種意思表達得清清楚楚:當 時,帶進去, ;當 時,帶進去, 。這種表達在以後寫似然函式的時候,非常有用,使得你不用同時寫好幾個公式。 白努力分佈的期望和方差都挺好算的:
白努力分佈很簡單,就是0-1分佈。我們用柱狀圖就能很好地表示出來。
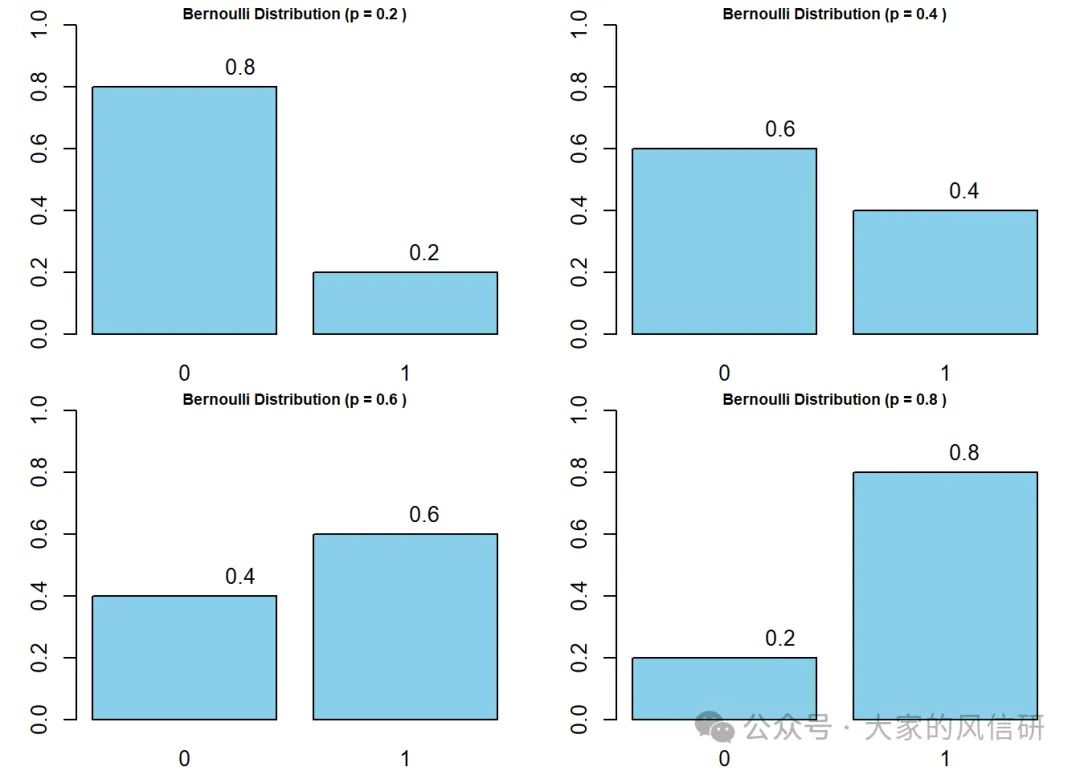
這0-1分佈啊,就像我們人生中的好多事情,拋開事實不談,不就是兩種結果麼?成功或者失敗,然後再加上個機率。這種表達一次成功或失敗的機率分佈,的確不用很深刻地去理解。范仲淹先生不是說麼“不以物喜不以己悲”,徐志摩同學也說過“得之我幸不得我命”。一次的成功或失敗,加強人生舞臺上作為一個演員的自我修煉就好了。畢竟,人生不是一次事件決定的。但,萬一一輩子,一直失敗,我是說萬一哈,那值得思考了。
我們把問題簡化和具象一些吧。假設我們人生經歷的事情是一個序列 ,這些事情是相互獨立的且每個事情都只有兩種狀態,成功1,失敗0.然後所有成功的機率都是 。問,那些0-1隨機變數的總和, 的機率分佈是怎麼樣的。於是,我們得出了0-1分佈的集合變身---二項分佈。(小時候看過那個集合變身的動畫片吧?組成腳和腿,組成軀幹和手臂,我來組成頭部...)
如果隨機變數 服從以 為引數的白努力分佈, ,那麼 服從以 , 為引數的二項分佈。由於 在成功時候取1,失敗時候取0,那麼這個 加和組成的 ,你完全可以當成成功的次數。
記住了二項分佈是白努力的組合變身,那麼他的期望和方差,也自然而然就記住了。
這種組合,還可以再升級一個版本:如果隨機變數 服從引數為 , 的二項分佈,那麼 則服從以 和 為引數的二項分佈。這些性質,極大地方便了二項分佈的應用。
我們來看看二項分佈隨引數變化的樣子吧。老規矩,兩個引數,我們先固定一個,看另一個變化導致的形狀變化。先固定p,看n的變化。
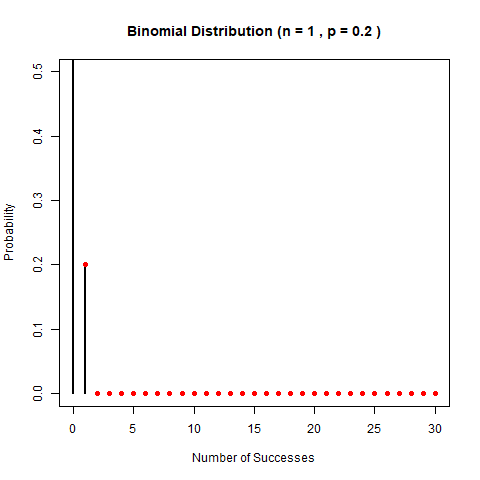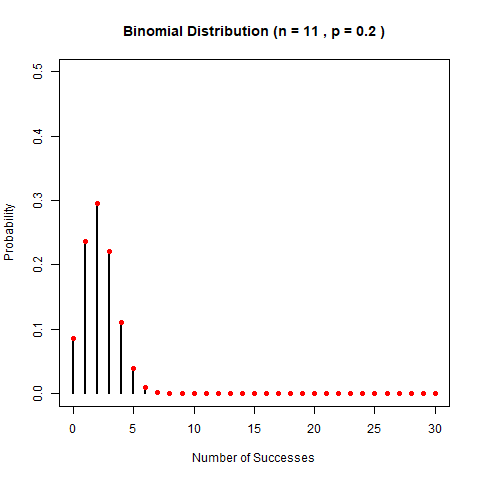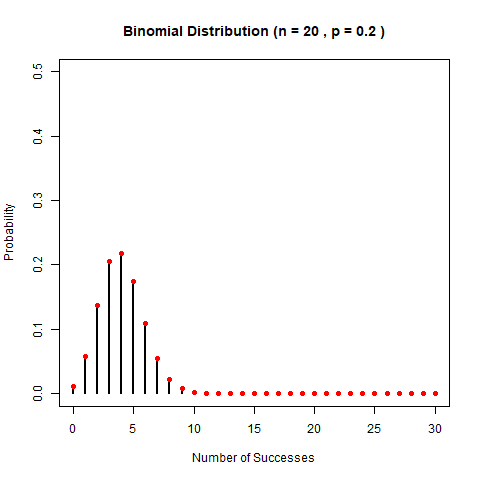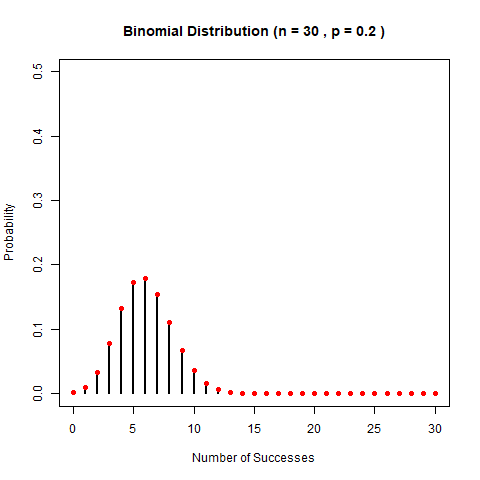
再固定n,看p的變化。
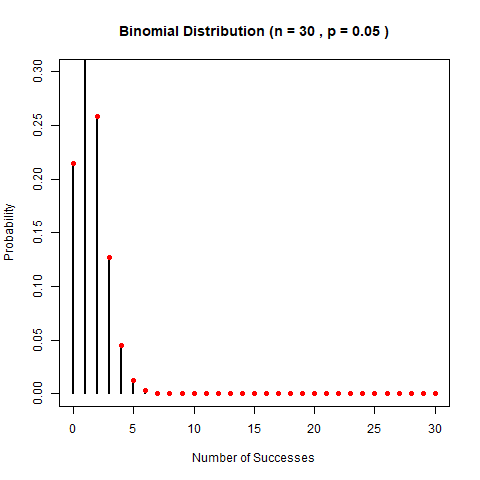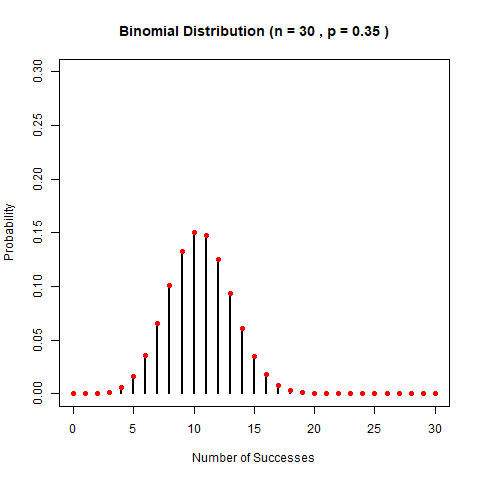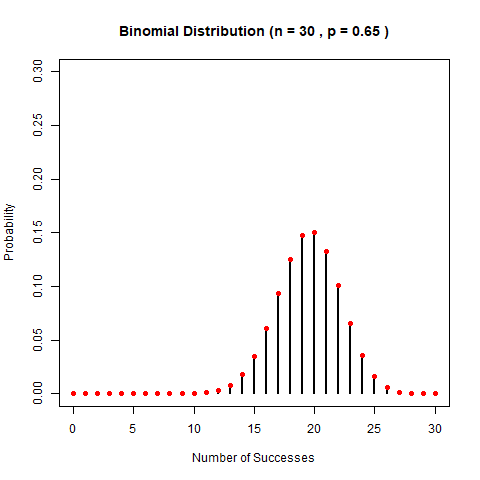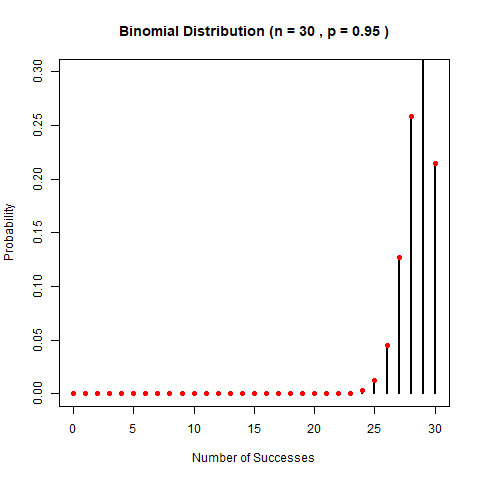
白努力和二項分佈最著名的應用,應該就是group testing了。爲了紀念5年前的那段經歷,我們寫一個當時背景下的例子吧:疫情下,爲了保護人民生命財產安全,大家都要做核酸。設某大學有1000名學生。一次核酸試劑測試20塊錢。已知xx疫情的感染率是0.02%。問,如何做核酸才能保證準確和經濟?
當然,土豪如你的校長可以大手一會,說“做,大家都做。1000乘以20也不過20000的事兒。”
嗯,行,這能保證準確。全員來一次,也不過20000塊錢的事兒。
但,很快,校長同志就頂不住了。一天20000倒是小事兒,但是架不住天天要做啊?
於是,100天以後,他哭著抱著統計系老師的大腿說“求您想想辦法吧!”
統計老師輕輕撫摸著校長的頭,說:“哭有錘子用,看老子給你弄得巴適。”(你看,多麼浪漫的想象啊...)
於是,統計老師掐指一算:每個人有兩種狀態,感染1,非感染0,感染機率是0.0002。那麼每個人的狀態服從白努力分佈 。1000個人,如果做1000次試劑測試,那麼我們可以知道 ,服從 的二項分佈。我們期望感染人數為1000乘以0.0002=0.2人,我們有很大可能一個人都不感染。
哎呀,爲了一個0.2的期望,每次花20000塊錢做檢測,即使政治再正確,經濟也受不了啊。OK,我們得想點辦法。
統計老師接著說,那,不如我們這樣,先講1000人分成10組,每組100人。然後把100人的核酸棉籤取樣液都抽出一點混在一起測一次。這樣,我們測10次就能測完1000人。這時,如果某組發現感染者,再對這一組全員進行的核酸棉籤取樣液進行測試。這樣,最少我們花200塊錢做10次,最多花20200做1010次就能搞定。
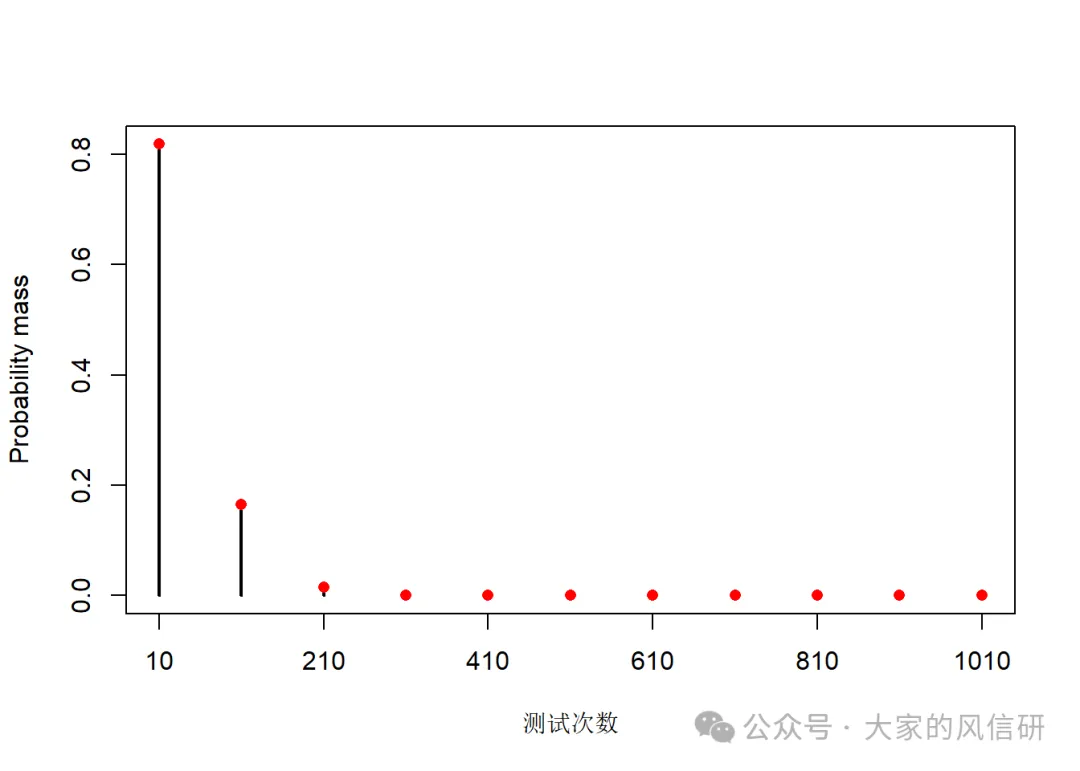
我們再認真算一下:設 是第 組的情況,那麼 包含有感染者1和無感染者0兩種狀態。有感染者狀態的機率為 。於是 。而10組的狀態就服從二項分佈 。那麼我們要測試的次數就是 (比如Y=2,說明兩組有感染者,那麼要測試的次數就是200),由於 ,所以分組的期望測次數就是 次。再加上我們必須要測的10次,分組混合條件下,平均只需要測試30次,600塊錢就能搞定了。
我們把測量次數的機率分佈畫一下。你可以看到,最壞的情況,我們需要測1010次,出現的機率9.261e-18,這幾乎是不可能事件。即使是測310次,機率也才8.098e-04。大部分情況下,我們只需要10次(p=0.819)或者110次(p=0.165)。
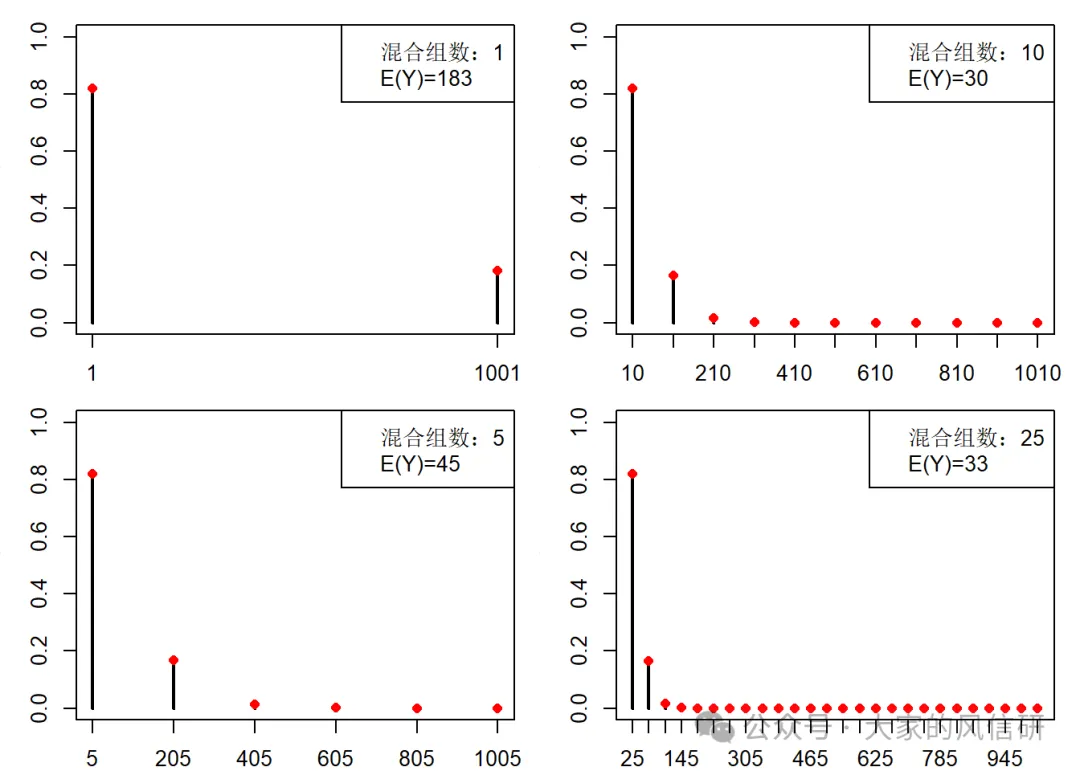
剛纔把1000人分成10組,我們只是隨意地分了一下。再稍微拓展一點,按照這個計算方法,看看分成更少的組數或者更多的組數會是怎麼樣呢?
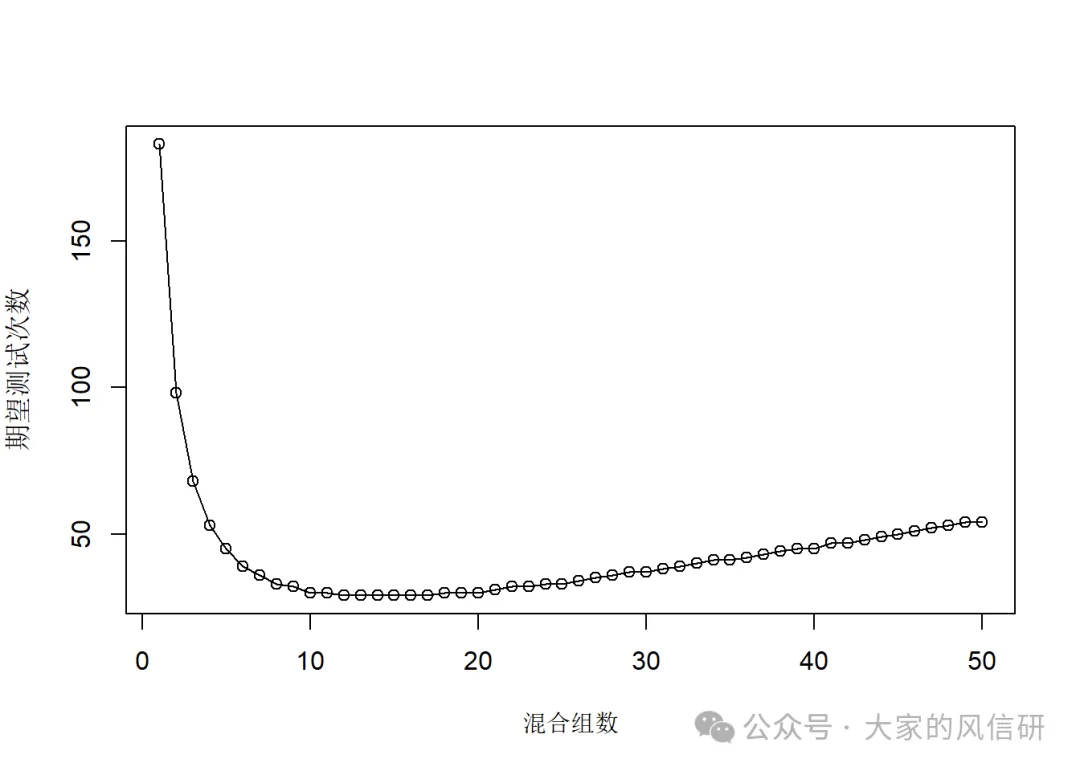
將混合組數與期望測試次數做一個散點圖,就能清晰地瞭解,1000個人我們分多少組進行測試最具有經濟性了。從圖中我們可以看到,分10-20組進行混合測試,是比較好的。大概30次左右測試就能搞定1000人了。
好啦,故事就到這裏了。統計老師幫校長解決了問題。校長感激不盡。從此,統計老師升職、加薪、迎娶白富美、走上人生巔峰...哈哈哈哈...(這只是一個故事哈,生活中,我們可以解決問題,但不能看到領導的脆弱)。但不管怎麼樣,我們看到了,白努力分佈,讓我們沒有白努力。lol
說起了疫情,我們都是幸運的。我想到了一些人。我把當時寫的文字留在這裏吧。爲了紀念,爲了忘卻的紀念。
時代的---紀念李醫生和他們
題記:人只因爲疼痛而流淚,不會因為白細胞的死而哭。
當你不屬於你,
便可勇往直前,無所畏懼。
當你真屬於你,
也會義無反顧,前赴後繼。
可是人啊,總是在是你非你之間猶豫,
於是大了聲音,小了記憶。
當我不屬於我,
便可淡看風雲,盡得其所。
當我真屬於我,
也會目營心匠,洞若觀火。
可是人啊,總是在是我非我之間蹉跎,
於是難得糊塗,模稜兩可。
這地球在轉啊轉,轉啊轉,重複著,重複著。
這世界在變啊變,變啊變,在試錯,在試錯。
像湖面一粒石子的波,
像託體同山阿的輓歌,
蝴蝶不一定是效應,也可能是莊生曉夢的傳說。
明天太陽會照著英雄的紀念碑,
十年後誰的回憶裡殘留著餘悲?
都是統計的樣本,都是歷史的菸灰。
都在時代中消逝,都在紅塵裡紛飛。
可是,
微斯人,吾誰與歸!
半夜寫專案本子,寫不下去時,突然想起了李醫生。他和我同年,都是東北人,都在武漢。他已經去了,雖然可能什麼都沒改變。我在寫本子,可能也不會改變什麼。但我們都想讓這個時代更美好一些。真實和美好,是歷史的塵埃都想努力的原因吧。2020.04
完結










0則評論