文章概要:作者用幽默詼諧的語言,貼近生活的案例,深入淺出地介紹了統計學的兩個重要不等式馬爾科夫不等式和切比雪夫不等式。
開篇宣告:1:以下內容轉自微信公眾號蔣新宇 大家的風信研《【人間的統計學】中心極限定理前傳:馬爾科夫不等式和切比雪夫不等式》,如有侵權,可聯絡刪除
2. 以下觀點,僅代表作者個人觀點,請帶著質疑的態度去閱讀。如有問題,歡迎評論區留言或直接聯絡作者
【人間的統計學】中心極限定理前傳:馬爾科夫不等式和切比雪夫不等式
在給一年級的小朋友上課時,我總會告訴大家,“知道大學和初中高中有什麼不同麼?初中高中是透過常量認識世界,大學是透過變數把握世界。初中高中是透過確定性理解世界,大學是透過不確定性探索世界。初中高中是透過等式展示真理,大學是透過不等式逼近真理...”
萌新小朋友們通常會先有些懵。這時,我就會繼續告訴大家“比如哈,你們雖然懂得 是常量運算, 是變數運算,但殊不知大學的變數,不止一個數的變,而是一個體系的變化。這個,當你們學特徵提取、主成分分析,透過座標系的變換將一組資料完全變成另一組資料時,就會深刻明白了。”
“至於確定性和不確定性,這個比喻更簡單,就是:高中、初中你成績好就確定地考上好大學,大學你成績好也不確定能找到好工作。什麼?你說成績好、情商高、會努力、會社交找到好工作的機率就會高。恭喜你,你涉及了迴歸分析的機率本質。這個,我們學回歸分析時候再談。”
“那麼,關於等式和不等式呢?”
“好,今天的課程,我們就來聊聊兩個重要的不等式...”
“切~,我還以為要和我們聊天呢?結果還是學習”
“人生,就是學習......”
我們有一堆資料,我們要認識和把握這堆資料。人的精力是有限的,我總不能一個一個數都記住吧,只能把這堆資料總結、簡化成幾個特徵維度。比如,描述資料集中趨勢的均值,描述資料分散趨勢方差,描述資料分佈特徵的偏度、峰度等等。透過這些特徵,我們不需要記住每一個數據,就能把握這堆資料的整體情況。這其中,如我一直強調,均值,是所有特徵之首。一堆資料,只要你把握均值,就把握了這堆資料的一半特徵了。【人間的統計學】資料的統計特徵:讓我們重新認識均值、方差這些東西
但問題來了。憑什麼說均值是資料的主要特徵呢?憑什麼說均值代表資料的集中趨勢呢?我知道均值之後,不過也就知道一個值麼?除了這個之外,我還能知道什麼資訊呢?
好,爲了回答這個問題,我們請出馬爾科夫不等式。
馬爾可夫不等式(Markov Inequality)
-
定義:對於非負隨機變數 和任意 (For a non-negative random variable and any ),有
-
解釋:用於估計隨機變數取大值的機率上限。
-
例子:設 ,則 。
馬爾科夫不等式表達了均值和所有資料的關係。如例子所示,當一堆資料,均值是1時,那麼這堆資料中大於100的資料不會超過1/100。馬爾科夫不等式直接給出了隨機變數最大取值的機率性上限,表達了所有資料需要圍繞在均值身邊,確定了均值的領導核心地位。當我們知道均值之後,資料的最大值,也基本上能依機率給出個範圍了。
雖然這個不等式很簡單,但其實還挺好用的,尤其是我年輕時,在網上和一幫渣渣就國家大事互噴的時候。論題通常是這樣:我國的平均工資為 元/月。但網上鋪天蓋地的月薪超過 元/月者,是不是真的?作為一個上過大學的選手,我們首先得計算一下。
-
設定變數:
-
設 為個人的月工資, 。 -
期望值 元/月。 -
設定 元/月。 -
應用不等式:
結論:根據馬爾科夫不等式,工資超過 20000 元/月的人口比例不超過。25%。這意味著,最多有約四分之一的人口月工資超過 20000 元。
馬爾科夫給了我怒懟網上人人月薪超20000的勇氣,但這勇氣似乎也不多,這也是沒辦法的事情,誰叫馬爾科夫只給了一個寬泛的上限呢。“最多有約四分之一的人口月工資超過 20000 元。”,萬一我碰到的對手就是這1/4裡面的呢。這時,就得改變噴他們的策略,不能見到說人人20000的就噴,見4個噴3個,也算是有理論依據了。
唉,那都是年輕時候的事情了。現在的我,早已不上網打嘴架了,沒有天涯了,沒有校內網了,不看抖音、不看小紅書,偶爾看看微信,通常還是工作的事情。我是不是老了......
說回馬爾科夫不等式,它表達了均值的重要性,但卻只是對非零變數的上限的約束,能不能給均值配個副手,讓均值的代表性更強一些呢?能,那就方差吧。讓我們請出切比雪夫不等式。
切比雪夫不等式(Chebyshev Inequality)
-
定義:對於隨機變數 和任意 (For a random variable and any ),有
-
解釋:用於估計隨機變數偏離其均值的機率上限。
-
例子:設 的方差為 1,則 。
有了方差的輔佐,均值的老大地位,更進一步得到了彰顯。切比雪夫不等式說,你們可以偏離均值,但偏離均值是有個上限滴。把上面的等式設成 時:
我們就會得到更廣泛流傳的切比雪夫不等式表達:不管怎麼分佈,資料偏離均值2倍標準差的機率不會超過25%(k=2),也就是說,至少有75%的資料會在均值加減2倍標準差範圍內。k=3等以此類推。
再給個例子吧。我們還繼續和人均20000的網路噴噴們討論工資。假設的月平均工資為 元,標準差為 元。我們想知道:工資偏離平均工資超過 元的機率上限是多少?
1:確定 : 偏離幅度 元。
2:應用切比雪夫不等式
結論:工資偏離平均工資超過 元的機率不超過 。換句話說,至少有 的機率工資在 範圍內。
“猶記少年輕狂時,橫掃跟帖意未知,“雙夫”在手噴天下,誰敢與吾論工資?”哈哈,都付笑談中...
但,記住馬爾科夫不等式和切比雪夫不等式對均值重要性的貢獻,總是好的。有了它們,大數定律就水到渠成了。而後麵的中心極限定理更是完整地給出了從樣本均值推斷總體均值路徑。從此,我們不僅知道了均值對一堆資料的代表性,而且還能透過少數樣本資料推斷出這種極具代表性的總體特徵。數理統計,開始從充滿賭博的機率論中走了出來,大殺四方......
還是延續【人間的統計學】的習慣,每章都需要一些圖,讓理解更容易些一些。這一次,我做了一個更高階的,可以互動的程式。我把他掛在了shinyapps.io上了:https://jxy119.shinyapps.io/Chapter6/。不知道這個連結在公眾號中是不是能直接開啟,如果打不開,複製到瀏覽器裡面就行了。介面如下所示。大家進去玩一下,去“看見理論”。
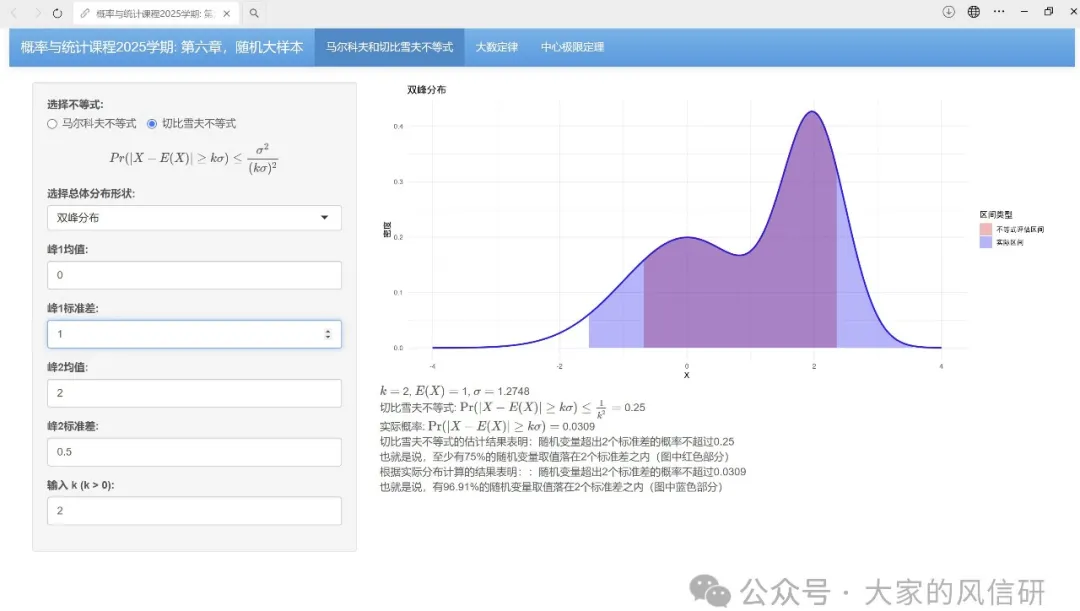
第一次用rmarkdown寫公眾號,出圖和公式編輯方便了很多,但排版有點費勁~~。另外shinyapps.io好像有流量控制,如果太多人登陸,可能就登陸不上了。以後,有空我們自己弄個伺服器就好了。
完結











0則評論