文章概要:作者用幽默诙谐的语言,贴近生活的案例,深入浅出地介绍了统计学的两个重要不等式马尔科夫不等式和切比雪夫不等式。
开篇声明:1:以下内容转自微信公众号蒋新宇 大家的风信研《【人间的统计学】中心极限定理前传:马尔科夫不等式和切比雪夫不等式》,如有侵权,可联系删除
2. 以下观点,仅代表作者个人观点,请带着质疑的态度去阅读。如有问题,欢迎评论区留言或直接联系作者
【人间的统计学】中心极限定理前传:马尔科夫不等式和切比雪夫不等式
在给一年级的小朋友上课时,我总会告诉大家,“知道大学和初中高中有什么不同么?初中高中是通过常量认识世界,大学是通过变量把握世界。初中高中是通过确定性理解世界,大学是通过不确定性探索世界。初中高中是通过等式展示真理,大学是通过不等式逼近真理...”
萌新小朋友们通常会先有些懵。这时,我就会继续告诉大家“比如哈,你们虽然懂得 是常量运算, 是变量运算,但殊不知大学的变量,不止一个数的变,而是一个体系的变化。这个,当你们学特征提取、主成分分析,通过坐标系的变换将一组数据完全变成另一组数据时,就会深刻明白了。”
“至于确定性和不确定性,这个比喻更简单,就是:高中、初中你成绩好就确定地考上好大学,大学你成绩好也不确定能找到好工作。什么?你说成绩好、情商高、会努力、会社交找到好工作的几率就会高。恭喜你,你涉及了回归分析的概率本质。这个,我们学回归分析时候再谈。”
“那么,关于等式和不等式呢?”
“好,今天的课程,我们就来聊聊两个重要的不等式...”
“切~,我还以为要和我们聊天呢?结果还是学习”
“人生,就是学习......”
我们有一堆数据,我们要认识和把握这堆数据。人的精力是有限的,我总不能一个一个数都记住吧,只能把这堆数据总结、简化成几个特征维度。比如,描述数据集中趋势的均值,描述数据分散趋势方差,描述数据分布特征的偏度、峰度等等。通过这些特征,我们不需要记住每一个数据,就能把握这堆数据的整体情况。这其中,如我一直强调,均值,是所有特征之首。一堆数据,只要你把握均值,就把握了这堆数据的一半特征了。【人间的统计学】数据的统计特征:让我们重新认识均值、方差这些东西
但问题来了。凭什么说均值是数据的主要特征呢?凭什么说均值代表数据的集中趋势呢?我知道均值之后,不过也就知道一个值么?除了这个之外,我还能知道什么信息呢?
好,为了回答这个问题,我们请出马尔科夫不等式。
马尔可夫不等式(Markov Inequality)
-
定义:对于非负随机变量 和任意 (For a non-negative random variable and any ),有
-
解释:用于估计随机变量取大值的概率上限。
-
例子:设 ,则 。
马尔科夫不等式表达了均值和所有数据的关系。如例子所示,当一堆数据,均值是1时,那么这堆数据中大于100的数据不会超过1/100。马尔科夫不等式直接给出了随机变量最大取值的概率性上限,表达了所有数据需要围绕在均值身边,确定了均值的领导核心地位。当我们知道均值之后,数据的最大值,也基本上能依概率给出个范围了。
虽然这个不等式很简单,但其实还挺好用的,尤其是我年轻时,在网上和一帮渣渣就国家大事互喷的时候。论题通常是这样:我国的平均工资为 元/月。但网上铺天盖地的月薪超过 元/月者,是不是真的?作为一个上过大学的选手,我们首先得计算一下。
-
设定变量:
-
设 为个人的月工资, 。 -
期望值 元/月。 -
设定 元/月。 -
应用不等式:
结论:根据马尔科夫不等式,工资超过 20000 元/月的人口比例不超过。25%。这意味着,最多有约四分之一的人口月工资超过 20000 元。
马尔科夫给了我怒怼网上人人月薪超20000的勇气,但这勇气似乎也不多,这也是没办法的事情,谁叫马尔科夫只给了一个宽泛的上限呢。“最多有约四分之一的人口月工资超过 20000 元。”,万一我碰到的对手就是这1/4里面的呢。这时,就得改变喷他们的策略,不能见到说人人20000的就喷,见4个喷3个,也算是有理论依据了。
唉,那都是年轻时候的事情了。现在的我,早已不上网打嘴架了,没有天涯了,没有校内网了,不看抖音、不看小红书,偶尔看看微信,通常还是工作的事情。我是不是老了......
说回马尔科夫不等式,它表达了均值的重要性,但却只是对非零变量的上限的约束,能不能给均值配个副手,让均值的代表性更强一些呢?能,那就方差吧。让我们请出切比雪夫不等式。
切比雪夫不等式(Chebyshev Inequality)
-
定义:对于随机变量 和任意 (For a random variable and any ),有
-
解释:用于估计随机变量偏离其均值的概率上限。
-
例子:设 的方差为 1,则 。
有了方差的辅佐,均值的老大地位,更进一步得到了彰显。切比雪夫不等式说,你们可以偏离均值,但偏离均值是有个上限滴。把上面的等式设成 时:
我们就会得到更广泛流传的切比雪夫不等式表达:不管怎么分布,数据偏离均值2倍标准差的概率不会超过25%(k=2),也就是说,至少有75%的数据会在均值加减2倍标准差范围内。k=3等以此类推。
再给个例子吧。我们还继续和人均20000的网络喷喷们讨论工资。假设的月平均工资为 元,标准差为 元。我们想知道:工资偏离平均工资超过 元的概率上限是多少?
1:确定 : 偏离幅度 元。
2:应用切比雪夫不等式
结论:工资偏离平均工资超过 元的概率不超过 。换句话说,至少有 的概率工资在 范围内。
“犹记少年轻狂时,横扫跟帖意未知,“双夫”在手喷天下,谁敢与吾论工资?”哈哈,都付笑谈中...
但,记住马尔科夫不等式和切比雪夫不等式对均值重要性的贡献,总是好的。有了它们,大数定律就水到渠成了。而后面的中心极限定理更是完整地给出了从样本均值推断总体均值路径。从此,我们不仅知道了均值对一堆数据的代表性,而且还能通过少数样本数据推断出这种极具代表性的总体特征。数理统计,开始从充满赌博的概率论中走了出来,大杀四方......
还是延续【人间的统计学】的习惯,每章都需要一些图,让理解更容易些一些。这一次,我做了一个更高级的,可以互动的程序。我把他挂在了shinyapps.io上了:https://jxy119.shinyapps.io/Chapter6/。不知道这个链接在公众号中是不是能直接打开,如果打不开,复制到浏览器里面就行了。界面如下所示。大家进去玩一下,去“看见理论”。
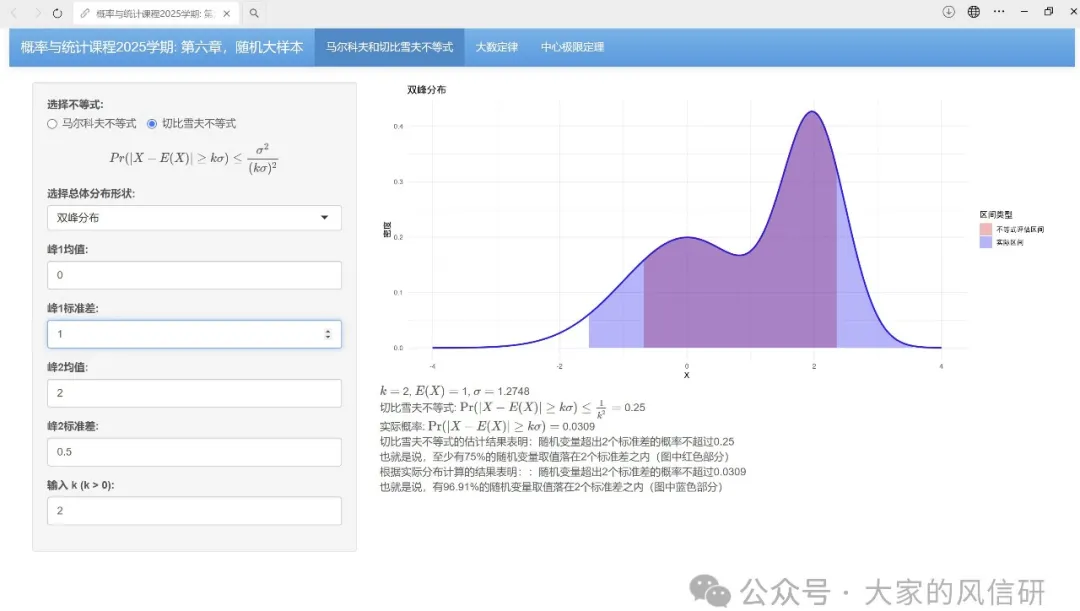
第一次用rmarkdown写公众号,出图和公式编辑方便了很多,但排版有点费劲~~。另外shinyapps.io好像有流量控制,如果太多人登陆,可能就登陆不上了。以后,有空我们自己弄个服务器就好了。
完结











0条评论